4 Team Round Robin Tournament

Type of sports tournament

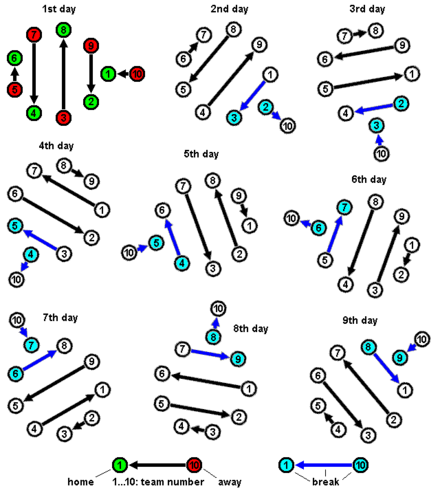
Example of a circular-robin tournament with 10 participators

A circular-robin tournament (or all-go-away-tournament) is a competition in which each contestant meets every other participant, usually in turn.^{[1] [2]} A circular-robin contrasts with an elimination tournament, in which participants/teams are eliminated later a sure number of losses.

Terminology [edit]

The term round-robin is derived from the French term ruban, meaning "ribbon". Over a long catamenia of time, the term was corrupted and idiomized to robin.^{[3] [4]}

In a unmarried circular-robin schedule, each participant plays every other participant one time. If each participant plays all others twice, this is oftentimes called a double round-robin. The term is rarely used when all participants play one some other more than twice,^[1] and is never used when i participant plays others an unequal number of times (as is the case in well-nigh all of the major United States professional sports leagues – come across AFL (1940–41) and All-America Football Conference for exceptions). In the Uk, a round-robin tournament has been called an American tournament in sports such every bit lawn tennis or billiards which usually take knockout tournaments, although this is now rarely, if ever, done.^{[5] [vi] [seven]} In Italian it is called girone all'italiana (literally "Italian-way group"). In Serbian it is called the Berger arrangement ( Бергеров систем , Bergerov sistem ), later on chess player Johann Berger. In Brazil it is called ( sistema de pontos corridos ), referring to the aggregating of accounted points equally the determinant of each participant's final performance, once all participants accept played their games.

A round-robin tournament with iv players is sometimes called "quad" or "foursome".^[8]

Use [edit]

In sports with a large number of competitive matches per flavour, double round-robins are common. Nigh clan football game leagues in the earth are organized on a double circular-robin basis, in which every team plays all others in its league once at home and in one case abroad. This system is also used in qualification for major tournaments such as the FIFA World Cup and the continental tournaments (eastward.g. UEFA European Championship, CONCACAF Gold Cup, AFC Asian Cup, CONMEBOL Copa América and CAF Cup of Nations). In that location are also round-robin bridge, chess, draughts, get, water ice hockey, curling, and Scrabble tournaments. The World Chess Championship decided in 2005 and in 2007 on an viii-actor double circular-robin tournament where each player faces every other player once equally white and one time equally black.

In a more farthermost case, the KBO League of baseball plays a 16-fold round robin, with each of the 10 teams playing each other xvi times for a total of 144 games per squad.

Group tournaments rankings usually go by number of matches won and drawn, with any of a variety of tiebreaker criteria.

Frequently, pool stages within a wider tournament are conducted on a round-robin footing. Examples with single round-robin scheduling include the FIFA World Cup, UEFA European Football Championship, and UEFA Cup (2004–2009) in football, Super Rugby (rugby wedlock) in the Southern Hemisphere during its by iterations as Super 12 and Super 14 (but not in its afterward 15- and xviii-team formats), the Cricket Globe Cup along with Indian Premier League, major Twenty-20 Cricket tournament, and many American Football game higher conferences, such as the Big 12 (which currently has 10 members). The group phases of the UEFA social club competitions and Copa Libertadores are contested as a double round-robin, every bit are well-nigh basketball game leagues exterior the U.s.a., including the regular season of the EuroLeague (likewise as its onetime Top 16 phase); the United Football League has used a double round-robin for both its 2009 and 2010 seasons.

Flavor ending tennis tournaments likewise use a round robin format prior to the semi on stages.

Evaluation [edit]

Advantages of the format [edit]

The champion in a round-robin tournament is the contestant that wins the most games, except when draws are possible.

In theory, a round-robin tournament is the fairest way to determine the champion from amidst a known and stock-still number of contestants. Each contestant, whether player or team, has equal chances against all other opponents because there is no prior seeding of contestants that volition preclude a friction match betwixt whatever given pair. The element of luck is seen to be reduced as compared to a knockout organisation since 1 or two bad performances need not ruin a competitor's chance of ultimate victory. Concluding records of participants are more authentic, in the sense that they represent the results over a longer menstruation against the same opposition.

The system is also improve for ranking all participants, not just determining the winner. This is helpful to determine the final rank of all competitors, from strongest to weakest, for purposes of qualification for another stage or competition as well as for prize money.

In team sport the (round-robin) major league champions are mostly regarded as the "all-time" team in the state, rather than the (elimination) loving cup winners.

Moreover, in tournaments such as the FIFA or ICC Globe Cups, a first round stage consisting of a number of mini round robins betwixt groups of 4 teams guards against the possibility of a team travelling possibly thousands of miles only to be eliminated later on just i poor performance in a straight knockout organisation. The top one, two, or occasionally iii teams in these groups so proceed to a straight knockout stage for the remainder of the tournament.

In the circumvolve of death (see beneath), it is possible that no champion emerges from a round-robin tournament, fifty-fifty if in that location is no draw. However, most sports have tie-breaker systems which resolve this.

Disadvantages of the format [edit]

Circular-robins can suffer from being too long compared to other tournament types, and with later scheduled games potentially not having any substantial meaning. They may as well require tiebreaking procedures.

Swiss system tournaments attempt to combine elements of the circular-robin and emptying formats, to provide a worthy champion using fewer rounds than a round-robin, while assuasive draws and losses.

Tournament length [edit]

The main disadvantage of a round robin tournament is the time needed to consummate it. Unlike a knockout tournament where half of the participants are eliminated after each circular, a circular robin requires one round less than the number of participants. For example, a tournament of xvi teams tin can be completed in just 4 rounds (i.eastward. xv matches) in a knockout (single elimination) format; a double elimination tournament format requires xxx (or 31) matches, but a round-robin would require fifteen rounds (i.eastward. 120 matches) to stop if each competitor faces each other once.

Other bug stem from the deviation betwixt the theoretical fairness of the round robin format and practice in a existent issue. Since the victor is gradually arrived at through multiple rounds of play, teams who perform poorly, who might accept been quickly eliminated from title contention, are forced to play out their remaining games. Thus games are played belatedly in the contest betwixt competitors with no remaining risk of success. Moreover, some later matches will pair 1 competitor who has something left to play for confronting some other who does non. Information technology may also exist possible for a competitor to play the strongest opponents in a round robin in quick succession while others play them intermittently with weaker opposition. This asymmetry means that playing the same opponents is not necessarily completely equitable.

There is also no scheduled showcase final match unless (by coincidence) ii competitors meet in the last match of the tournament, with the result of that match determining the championship. A notable example of such an issue was the 1950 FIFA World Cup match between Uruguay and Brazil.

Qualified teams [edit]

Further problems arise where a round-robin is used as a qualifying round within a larger tournament. A competitor already qualified for the next stage before its last game may either not endeavour hard (in society to conserve resources for the next stage) or even deliberately lose (if the scheduled next-phase opponent for a lower-placed qualifier is perceived to exist easier than for a higher-placed one).

Iv pairs in the 2012 Olympics Women'southward doubles badminton, having qualified for the side by side round, were ejected from the competition for attempting to lose in the round robin phase to avert compatriots and better ranked opponents.^[nine] The round robin phase at the Olympics was a new introduction, and these potential problems were readily known prior to the tournament; changes were fabricated prior to the side by side Olympics to prevent a repeat of these events.

Circle of death [edit]

Another disadvantage, especially in smaller circular-robins, is the "circle of death", where teams cannot exist separated on a head-to-head record. In a three-team round-robin, where A defeats B, B defeats C, and C defeats A, all iii competitors will accept a record of one win and one loss, and a tiebreaker will need to be used to divide the teams.^[10] This famously happened during the 1994 FIFA World Cup Group East, where all four teams finished with a record of one win, ane draw, and ane loss. This phenomenon is analogous to the Condorcet paradox in voting theory.

Scheduling algorithm [edit]

If ${\displaystyle n}$ is the number of competitors, a pure round robin tournament requires ${\displaystyle {\begin{matrix}{\frac {n}{ii}}\end{matrix}}(n-1)}$ games. If ${\displaystyle north}$ is even, and then in each of ${\displaystyle (north-1)}$ rounds, ${\displaystyle {\brainstorm{matrix}{\frac {north}{2}}\end{matrix}}}$ games tin be run concurrently, provided at that place exist sufficient resources (east.thou. courts for a tennis tournament). If ${\displaystyle n}$ is odd, in that location will be ${\displaystyle n}$ rounds, each with ${\displaystyle {\brainstorm{matrix}{\frac {north-1}{2}}\end{matrix}}}$ games, and one competitor having no game in that circular.

Circle method [edit]

The circumvolve method is the standard algorithm to create a schedule for a round-robin tournament^{[ commendation needed ]}. All competitors are assigned to numbers, and and so paired in the first circular:

Round 1. (i plays fourteen, 2 plays thirteen, ... )

1	ii	iii	4	5	6	7
14	13	12	11	10	nine	eight

Adjacent, one of the competitors in the showtime or last column of the table is fixed (number one in this example) and the others rotated clockwise i position

Round 2. (ane plays 13, 14 plays 12, ... )

ane	14	2	3	4	v	6
xiii	12	eleven	10	9	8	vii

Round 3. (1 plays 12, 13 plays 11, ... )

ane	13	xiv	2	3	4	5
12	11	x	9	eight	seven	6

This is repeated until you end upwardly nigh back at the initial position:

Round 13. (1 plays 2, 3 plays 14, ... )

ane	3	4	five	6	vii	8
2	14	xiii	12	11	ten	ix

To come across that - with an even number ${\displaystyle n}$ of competitors - this algorithm realizes every possible combination of them (equivalently, that all pairs realized are pairwise dissimilar), nosotros argue as follows.

First, the algorithm obviously realizes every pair of competitors if 1 of them equals ${\displaystyle 1}$ (the non-moving competitor).

Next, for pairs of non- ${\displaystyle 1}$ competitors, let their distance be the number ${\displaystyle k<{\frac {n}{2}}}$ of times the rotation has to exist carried out in social club that one competitor arrives at the position the other had.

In the example given ( ${\displaystyle n=14}$ ), ${\displaystyle 2}$ has distance ${\displaystyle one}$ to ${\displaystyle iii}$ and to ${\displaystyle 14}$ and it has distance ${\displaystyle six}$ to ${\displaystyle 8}$ and to ${\displaystyle 9}$ .

In a round, a non-leftmost position (non including ${\displaystyle 1}$ ) tin can only be taken by competitors of a stock-still distance. In round ${\displaystyle 1}$ of the case, in the second position competitor ${\displaystyle 2}$ plays against ${\displaystyle 13}$ , their distance is ${\displaystyle 2}$ . In circular ${\displaystyle 2}$ , this position is held past competitors ${\displaystyle fourteen}$ and ${\displaystyle 12}$ , also having altitude ${\displaystyle 2}$ , etc. Similarly, the next position ( ${\displaystyle 3}$ against ${\displaystyle 12}$ in round ${\displaystyle ane}$ , ${\displaystyle 2}$ against ${\displaystyle 11}$ in round ${\displaystyle two}$ , etc.) can only agree altitude- ${\displaystyle 4}$ competitors.

For every ${\displaystyle k<{\frac {n}{2}}}$ , in that location are exactly ${\displaystyle n-1}$ pairs of distance ${\displaystyle k}$ . There are ${\displaystyle n-i}$ rounds and they all realize one distance- ${\displaystyle k}$ pair at the aforementioned position. Clearly, these pairs are pairwise dissimilar. The conclusion is that every distance- ${\displaystyle m}$ pair is realized.

This holds for every ${\displaystyle 1000}$ , hence, every pair is realized.

If there are an odd number of competitors, a dummy competitor can exist added, whose scheduled opponent in a given circular does not play and has a bye. The schedule can therefore be computed equally though the dummy were an ordinary player, either fixed or rotating.

Instead of rotating one position, any number relatively prime to ${\displaystyle (n-ane)}$ volition generate a complete schedule. The upper and lower rows tin can indicate domicile/abroad in sports, white/black in chess, etc.; to ensure fairness, this must alternate between rounds since competitor 1 is always on the first row. If, say, competitors 3 and 8 were unable to fulfil their fixture in the third round, information technology would need to be rescheduled outside the other rounds, since both competitors would already be facing other opponents in those rounds. More than complex scheduling constraints may require more complex algorithms.^[11] This schedule is practical in chess and draughts tournaments of rapid games, where players physically move round a table. In French republic this is called the Carousel-Berger system (Système Rutch-Berger).^[12]

The schedule tin can also be used for "asynchronous" round-robin tournaments where all games take place at different times (for example, considering there is only one venue). The games are played from left to right in each round, and from the first round to the final. When the number of competitors is fifty-fifty, this schedule performs well with respect to quality and fairness measures such as the amount of rest between games. On the other mitt, when the number of competitors is odd, it does non perform then well and a different schedule is superior with respect to these measures.^[13]

Berger tables [edit]

Alternatively Berger tables,^[14] named later the Austrian chess master Johann Berger, are widely used in the planning of tournaments ^[15] . Berger published the pairing tables in his two Schach-Jahrbücher (Chess Register),^{[16] [17]} with due reference to its inventor Richard Schurig.^{[18] [nineteen]}

Circular 1	1 – fourteen	2 – 13	iii – 12	4 – 11	5 – 10	6 – 9	7 – eight
Round 2	xiv – 8	9 – 7	10 – 6	11 – v	12 – 4	13 – 3	i – ii
Round 3	2 – 14	3 – ane	4 – 13	5 – 12	6 – 11	7 – 10	viii – ix
...	...
Circular 13	7 – 14	8 – 6	9 – 5	10 – 4	11 – 3	12 – ii	13 – i

This constitutes a schedule where histrion fourteen has a fixed position, and all other players are rotated counterclockwise ${\displaystyle {\frac {n}{2}}}$ positions. This schedule is easily generated manually. To construct the adjacent round, the last histrion, number 8 in the beginning round, moves to the head of the table, followed by role player 9 against player vii, player 10 against 6, until player 1 against actor 2. Arithmetically, this equates to calculation ${\displaystyle {\frac {n}{2}}}$ to the previous row, with the exception of thespian ${\displaystyle n}$ . When the result of the add-on is greater than ${\displaystyle (n-ane)}$ , then subtract ${\displaystyle (n-one)}$ from the sum.

This schedule tin can likewise be represented every bit a (north-one, n-one) table, expressing a circular in which players meets each other. For instance, actor seven plays against player 11 in round 4. If a player meets itself, then this shows a good day or a game confronting actor due north. All games in a round constitutes a diagonal in the tabular array.

Diagonal Scheme × 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 six vii 8 9 ten xi 12 13 1 ane 2 3 4 5 6 7 8 9 10 11 12 13 2 1 ii three 4 5 6 7 8 9 10 11 12 thirteen iii 1 2 3 4 5 6 7 8 9 10 11 12 13 4 1 ii 3 four 5 6 7 8 9 10 xi 12 13 v i 2 3 four v 6 7 viii 9 x xi 12 13 6 one 2 3 4 5 6 seven 8 nine x 11 12 13 7 1 2 3 iv five vi 7 8 9 10 11 12 xiii 8 i two 3 4 v 6 7 eight 9 x 11 12 13 nine 1 ii 3 iv five 6 vii 8 9 ten 11 12 13 10 ane 2 3 4 5 6 7 8 ix 10 11 12 13 eleven 1 two 3 iv 5 6 vii 8 9 10 11 12 13 12 ane 2 3 4 v six 7 eight 9 10 11 12 thirteen 13 one 2 three 4 5 half dozen seven 8 ix x 11 12 xiii

Round Robin Schedule × i 2 three 4 v 6 vii eight 9 10 xi 12 xiii 1 one 2 3 4 v half dozen 7 8 9 10 11 12 13 2 two iii four five 6 7 8 nine 10 11 12 xiii 1 3 3 iv 5 6 7 eight ix 10 11 12 13 1 2 iv 4 five 6 7 8 9 10 11 12 13 i 2 3 5 5 six vii 8 9 10 eleven 12 thirteen 1 2 three iv 6 6 7 viii 9 10 11 12 13 1 2 three iv v seven seven 8 9 ten 11 12 13 ane 2 iii iv 5 6 8 8 nine 10 11 12 thirteen ane 2 3 iv v 6 7 9 ix 10 11 12 13 i 2 3 4 5 6 seven 8 10 10 xi 12 13 i 2 3 4 five vi 7 8 nine 11 11 12 13 1 2 3 iv 5 half-dozen 7 8 9 ten 12 12 thirteen i ii iii 4 5 6 seven 8 9 x 11 13 xiii 1 ii 3 iv 5 half dozen 7 8 nine 10 11 12

The higher up schedule tin as well be represented by a graph, equally shown below:

Round Robin Schedule Span Diagram

Both the graph and the schedule were reported by Édouard Lucas in^[xx] every bit a recreational mathematics puzzle. Lucas, who describes the method as simple and ingenious, attributes the solution to Felix Walecki, a teacher at Lycée Condorcet. Lucas also included an alternative solution by means of a sliding puzzle.

Original construction of pairing tables by Richard Schurig (1886) [edit]

For an fifty-fifty number ${\displaystyle n}$ or an odd number ${\displaystyle north-1}$ of competitors, Schurig^[19] builds a table with ${\displaystyle n/2}$ vertical rows and ${\displaystyle n-1}$ horizontal rows. And so he populates information technology starting from the top left corner by repeating the sequence of numbers from one up to ${\displaystyle n-1}$ . Here is an instance tabular array for 7 or eight competitors:

Round 1	one	2	three	4
Round ii	five	6	7	1
Round iii	ii	3	4	5
Round 4	half dozen	7	ane	2
Round 5	three	iv	5	half dozen
Round 6	vii	1	2	3
Round 7	four	v	vi	7

So to go the opponents a 2d table is synthetic. Every horizontal row ${\displaystyle ten}$ is populated with the same numbers as row ${\displaystyle x+1}$ in the previous table (the last row is populated with numbers from the first row in the original tabular array), simply in the reverse social club (from right to left).

Round 1	– i	– seven	– 6	– 5
Round 2	– 5	– 4	– 3	– 2
Round 3	– ii	– 1	– 7	– 6
Round 4	– 6	– 5	– four	– 3
Circular 5	– 3	– 2	– i	– 7
Round 6	– 7	– 6	– v	– four
Round 7	– 4	– 3	– ii	– i

Past merging above tables we arrive at:

Round 1	1 – 1	two – 7	three – 6	four – 5
Circular two	5 – five	six – 4	7 – 3	1 – two
Circular 3	ii – 2	3 – 1	4 – vii	5 – 6
Circular 4	6 – 6	7 – 5	1 – 4	ii – 3
Round 5	3 – 3	iv – 2	five – 1	6 – 7
Circular vi	seven – 7	1 – vi	2 – five	3 – 4
Round 7	4 – 4	v – iii	6 – two	7 – 1

And then the first column is updated: if the number of competitors is even, player number ${\displaystyle n}$ is alternatingly substituted for the showtime and 2d positions, whereas if the number of competitors is odd a bye is used instead.

The pairing tables were published as an annex concerning the arrangements for the holding of main tournaments. Schurig did not provide a proof nor a motivation for his algorithm. For more than historical details, see Ahrens.^[21]

See also [edit]

• Grouping tournament ranking system, including details of tie-breaking systems
• Combinatorial design, a balanced tournament design of order due north (a BTD(northward))
• Tournament (graph theory), mathematical model of a round-robin tournament
• Other tournament systems:
  • Swiss system tournament
    • McMahon system tournament, a variation of the Swiss organisation that incorporates pre-tournament rankings to foreclose early on lopsided pairings
  • Single-elimination tournament
    • Shaughnessy playoff system, a type of single-elimination tournament featuring four teams
  • Double-emptying tournament
  • McIntyre Arrangement, a series of tournament formats that combine features of single- and double-elimination tournaments
• Bridge:
  • Duplicate bridge movements
• Chess:
  • List of round-robin chess tournaments
  • Scheveningen organization, where each member of i team plays each member of the other
• Voting:
  • Condorcet method
  • Condorcet criterion

References [edit]

1. ^ ^{a b} Webster'due south Third New International Dictionary of the English language, Unabridged (1971, G. & C. Merriam Co), p.1980.
2. ^ Orcutt, William Dana (1895). Official Backyard Tennis Bulletin. Vol. 2. New York: The Editors. pp. 1, 3.
3. ^ Strehlov, Richard A; Wright, Sue Ellen, eds. (1993). Standardizing Terminology for Better Communication: Exercise, Applied Theory, and Results. Vol. 1166. ASTM. pp. 336–337. ISBN0-8031-1493-1.
4. ^ Brewer's Lexicon of Phrase & Fable. New York: Harper & Brother Publishers. p. 786.
5. ^ "A Glossary of Terms Used in Connection with Billiards". Billiard Monthly. English Amateur Billiards Association. Feb 1912. Archived from the original on March 3, 2022. American Tournament: A tournament in which each thespian must meet in plough every other player.
6. ^ Centrolineal. "American tournament". Chambers 21st Century Dictionary. Allied Publishers. p. 38. ISBN978-0550106254 . Retrieved August i, 2012.
7. ^ Mead, Shepherd (1977). How to succeed in lawn tennis without actually trying: the piece of cake tennismanship way to practise all the things no tennis pro can teach y'all. McKay. p. 130. ISBN9780679507499 . Retrieved August ane, 2012.
8. ^ "An Introduction to USCF-Rated Tournaments" (PDF). The U.s.a. Chess Federation. Feb 23, 2006.
9. ^ "Eight Olympic badminton players butterfingers for 'throwing games'". The Guardian. August 1, 2012. Retrieved Baronial 1, 2012.
10. ^ "UC Berkeley Quiz Bowl: How To Brand Schedules". www.ocf.berkeley.edu.
11. ^ Dinitz, Jeff (November 13, 2004). "Designing Schedules for Leagues and Tournaments" (PDF). Abode Page for Jeff Dinitz. Mount Saint Mary College: GRAPH THEORY DAY 48.
12. ^ Le livre de l'arbitre : édition 2008 (PDF) (in French). Fédération Française des Échecs. 2008. p. 56. ISBN978-2-915853-01-8.
13. ^ Suksompong, Warut (2016). "Scheduling asynchronous circular-robin tournaments". Operations Research Letters. 44 (1): 96–100. arXiv:1804.04504. doi:10.1016/j.orl.2015.12.008. S2CID 4931332.
14. ^ Table de Berger (in French), examples of round robin schedules upwardly to 30 participants.
15. ^ "C. General Rules and Technical Recommendations for Tournaments / 05. General Regulations for Competitions / Full general Regulations for Competitions. Annex i: Details of Berger Tabular array /". FIDE Handbook. FIDE. (contents page)
16. ^ Berger, Johann (1893). Schach-Jahrbuch für 1892/93 (in German). Leipzig. pp. 26–31. OCLC 651254787.
17. ^ Berger, Johann (1899). Schach-Jahrbuch für 1899/1900 : Fortsetzung des Schach-Jahrbuches für 1892/93 (in German). Leipzig. pp. 21–27. OCLC 651254792.
18. ^ Richard Schurig (in French)
19. ^ ^{a b} Schurig, Richard (1886). "Dice Paarung der Theilnehmer eines Turniers". Deutsche Schachzeitung (in German language). 41: 134–137. OCLC 556959107.
20. ^ Lucas, Edouard (1883). "Les jeux de demoiselles". Récréations Mathématiques (in French). Paris: Gauthier-Villars. pp. 161–197.
21. ^ Ahrens, Wilhelm (1901). "Anordnungs Probleme, Aufgabe 2". Mathematische Unterhaltungen und Spiele (in German). Leipzig: B. G. Teubner. ark:/13960/t2w37mv93.

External links [edit]

• Round Robin Tournament Scheduling link to schedules (balanced,cyclic,showtime-fit,whist).
• Round Robin System Tables (Scoring - Programme)
• Costless Printable Round Robin Brackets

4 Team Round Robin Tournament,

Source: https://en.wikipedia.org/wiki/Round-robin_tournament

Posted by: jonessuas1985.blogspot.com

Share this post